さて、むしまるくさんところに、

「確率二分の一？」という問題が出されました。

実はこれはかなり有名な問題で、

モンティ・ホール問題と呼ばれています。

別名「モンティホールジレンマ」です。

これは、アメリカのクイズ番組の司会者のMonty Hallさんが担当しているコーナーから派生した問題です。

なぜ有名になったかというと、

1990年に "Parade magazine" の中の Marilyn vos Savant の

「Ask Marilyn」という質問と回答のコラムでこの問題の解が議論された後、

数百人の数学教授を含む約一万の読者が、（実際には正答であったにも関わらず）

「彼女の解答は間違っている」と投書したこと…らしい。ヽ(;´Д`)ノ

（＊ｂｙ モンティ・ホール問題のWIKIpedia）

で、解答なんですが、これも「モンティ・ホール問題」をグーグルで検索したら、

山のように出てきますね。

で、折角なので、ここはよくある数学、確率論やベイズの定理など方法ではなく、

私がKCGIで教えている経営学特論の意思決定メカニズムの章で紹介した、

ディシジョンツリーを使って説明してみます。

簡単に言うと、これは経済学のゲーム論の「ゲームの木」と似たようなものですね。
（＊これで皆さんが「簡単」と感じてくれるかどうかはめちゃ微妙だが…。）
（＊ゲームの木についてはKCGの経済学１で軽く触りました。）

まず、モンティ・ホール問題をおさらいします。

→koho通信から拝借。

あるクイズ番組がありました。

３つの扉があり，そのうち一つの奥にはクルマが置いてあって，
クルマのある扉を選べばもらえる，というものです。

普通に考えれば確率３分の１なのですが，このクイズには
ちょっとした仕掛けがあります。

回答者が選んだ扉の前に立ったときに，司会者が
残りの２つのうち，クルマがない扉を開けるのです！

ここで回答者は扉を変えることもできるし，
そのままにしておくこともできます。

変えたほうがよいのか，そのままの方がよいのか，
みなさんなら，どうされますかー？？

ここは「確率」ではなく、「期待値」としてこの問題をみます。

一応、景品の車の価値を￥１，２００，０００と仮定しましょう。

以上の仮定から、以下のようなディシジョンツリーを描くことが出来ます。

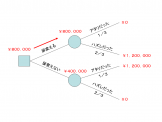
↓モンティ・ホール問題のディシジョンツリー

（＊以上の画像を、別ウィンドウで開いたまま、以下の説明文と同時に読むことをオススメします。）

ディシジョンツリーでは、

□は決定ノードと言って、行動の分岐を表しています。

○は確率ノードと言って、コントロールできない事象を表しています。

描くときは、左から右を描いて、各ノードや枝の状態を書き込み、

そして右から左に最適な意思決定を探ります。

今回では、意思決定ノードは：

１．どの扉を選ぶか
２．その後、扉を変えるかどうか

の二種類がありますが、

ここでは、どの扉を選んでも「同じよう」に扱って、

選んだ扉の「アタリ率」を確率ノードで表現するようにしました。

そして、一種類の決定ノード（扉変えるかどうか？）と、

一種類の確率ノード（最初の選択はアタリかどうか？）を用いて、

ディシジョンツリーを描きます。

で、とりあえず左端に決定ノードを描き、

このノードから二つの枝、「扉変える」、「扉変えない」を描きます。

このいずれの枝は、「現選択はアタリかどうか？」の確率ノードに繋ぎます。

そして、二つの確率ノードから、さらに「アタリだった」と「ハズレだった」の二つの枝に分岐します。

設定から、「最初でいきなりアタリ」の確率は三分の一で、

「最初からハズレ」の確率は三分の二ですね。

利得ですが、このように考えます。

「アタリだった」のに→「扉変える」→ハズレに成るので→￥０
「アタリだった」→「扉変えない」→アタリのままなので→￥１，２００，０００
「ハズレだった」→「扉変える」→アタリに成るので→￥１，２００，０００
「ハズレだった」のに→「扉変えない」→ハズレのままなので→￥０

ここまで出来たら、右から左へ検討していきます。

「扉変える」場合の確率ノード（上のほう）の期待利得を見てみると、
（￥０*１／３）＋（￥１，２００，０００*２／３）＝￥８００，０００

「扉変ない」場合の確率ノード（下のほう）の期待利得を見てみると、
（￥０*２／３）＋（￥１，２００，０００*１／３）＝￥４００，０００

で、更に左端の決定ノードを見ます。

この決定ノードの右上の枝の期待利得は￥８００，０００で、

右下の枝の期待利得は￥４００，０００です。

「￥８００，０００＞￥４００，０００」なので、

右上の枝、つまり「扉変える」ほうが、期待利得が高い…ということになりますね。

ちなみに、扉変える時の期待利得は変えない時の２倍…です（倍違い！）。

従いまして、モンティ・ホール問題において、

「扉を変えたほうがいい」というのが正しい意思決定になりますね。Ψ(`∇´)Ψ

正直、PPTやフラッシュなど動的コンテンツを使ったほうがず～っと説明しやすくて、

ブログ上でHTMLで説明するのはむずい…ですね。

ん～やっぱりEラーニングコンテンツをラクラク作成できるKCGはスゴイかも。

でも、まあ、じーっとにらめっこしてもらいましたら、

多分分かってもらえると思いますので、

これでよしとしましょう。(゜▽゜)

長々と、ご清聴ありがとうございました～(‘◇’)ゞ