Scilabはややこしい方程式を解くにも有効です。
exp(x)-x-2=0の解を求めるには
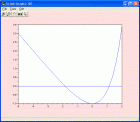
deff(‘y=f(x)’,’y=exp(x)-x-2′);fsolve(1,f) Enter とすれば,すぐに 1.1461932 と出てきます。deff で関数を定義すれば fsolve で解が求まります。ここで（ ）内の１はトライアルに与える初期値ですが，その値はｙ＝ｆ（ｘ）のグラフから読み取ります。ではグラフを描くには？ deff(‘y=f(x)’,’y=exp(x)-x-2′);x=[-5:0.1:2];plot(x,f);plot(x,0)
で図(Sorry! too faint)のようなグラフが描かれ、曲線とｘ軸の交点近くのｘ値である１を初期値に採るというわけ。交点はもうひとつあるので－１を採れば（－２でもOK）– 1.8414057という解が得らます。
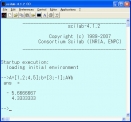
Scilabは数値計算用の便利なツールです。しかもフリー。コマンドまたは数行のスクリプト（というよりさらに小規模）を書くだけで、方程式の解、行列演算、数値積分、微分方程式、３Dグラフ描画などができます。しかし制御工学以外では知名度は低かったようで、聞いたことしかなかったが、この春から使ってみて気に入りました。図は連立方程式を解いているところです。A=[1,2;4,5];b=[3;-1];A\\b Enterで
x+2y=3
4x+5y=-1
の解がすぐに出てきます。筆算でやってみる気が起きるのは、未知数が２つの時だけですが、この方法だといくつでも同じこと。さらにこの後 spec(A) とするだけでAの固有値，固有ベクトルが求まります。いやぁ，昔，線形代数の勉強で苦労したし，授業を持ってからはもっと苦労した。それがたった１行でできてしまった。
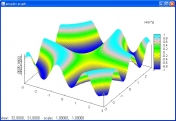
３Dプロットはgnuplotを使うのが一番便利のようです。プログラム，操作は簡単でソフトはロハだし。SASやScilabでもやってみたけど，やはりこれがオススメです。図は ｚ＝sin(xy) のグラフです。ただしｚ＝・・を与えて描画させるのはいいが，ファイルから数値を読む込むときは時間がかかりそうですが。
Myぐにゅぐにゅぎゃらりーへどうぞ
この人やっぱスゴイです。数学はピタゴラス，ユークリッド，・・・・デカルト，フェルマー，ニュートン，ガウス，コーシー，リーマン・・・という天才たちが頭に浮かびましたが，古代中国にこんな人がいたとは知らんかった。円周率の正確な値を求め，1000年以上も最高記録を保持していたのです。また暦学においても，1年や1月の日数などは現在の値とほぼ同じものを使って，閏を求めたようで，きっとヤヤコシイ計算が得意だったのしょうね。1500年前，日本では古墳時代、ヨーロッパではフンやゲルマンが暴れていたころのことです。これらを
Webにまとめたのでご覧ください。これらはKCG一般教育「自然科学史」のネタになります。
「和をもって貴しとし・・」で始まる17条の憲法は第3条までが総論で第4条から第16条までには役人豪族の心得が示されています。ところが，第17条は「それ事はひとり断（さだ）むべからず・・・」となって実は第１条の内容の繰り返しです。聖徳太子は同じことを最後に再び言っているのはなぜでしょうか？
大切だからくどく言った？ いやそうではなくて17という数にこだわってあえて追加したと思います。17とは何ともきりの悪い数で素数ですが，実は１７＝５＋７＋５です。日本語は五七五で綴ると非常にきれいにまとまります。和歌俳句に限らず「もしもし亀よ･･･」も「春のうららの･･･」も「月はおぼろに･･･」も七五調です。さすがは聖徳太子，きっと読む人の印象を考えて書いたのでしょうね！
昨年「博士の愛した数式」がTVでも映画でも話題になりました。80分しか記憶がもたない数学者が主人公で「220と284は友愛数だ」という台詞がありますね。これって何？実は素数，完全数，友愛数，それらはすべて約数の和で求まります。
例えば28の約数は1,2,4,7,14,28で自分自身を除いて合計すると1+2+4+7+14＝28となり元の数に戻ります。このような数を完全数といいます。13の場合は約数は1と13しかなく合計は1，このような数が素数です。12の場合,約数は1,2,3,4,6,12で同じように合計すると16で，特別な数ではありません。
220の約数の和は1+2+4+5+10+11+20+22+44+55+110=284で，その284の約数の和は1+2+4+71+142＝220。このような場合が互いに友愛数なのです。このような数は非常にまれで，順に探していくと10000までに完全数はわずか4個，6，28，496，8128で，また友愛数は(220 284)，(1184 1210)，(2924 2620)，(5020 5564),( 6232 6368)しかありません。遅いですが 計算サイトから求まります。
子供のころクラスの中に誕生日が同じ子がいるという思い出はありませんか？このようなことは50人の場合ではまず間違いなく起ります。30人でもかなり起りやすい現象です。１年は365日もあるのに不思議ですね。いや実は不思議でもなんでのないのです。
２択選択○×問題が10題をデタラメに答えて60点が取れないものでしょうか？その確率は40%近くもあります。
こんな問題を扱うのが統計学で、今期はMERでそれぞれの統計学を担当しています。サインコサインよりは役立つ数学です。単純だけどややこしい計算はコンピュータに任せて、直観力を養いましょう。