gnuplot 入門のページを作りました。
現在，電卓機能から３D描画まで載っています。順次加筆していきます。
ぐにゅ入門
KCG数値解析

　昨日は法事で奈良へ行ってきました。鴨川校の講師だったN先生の一周忌です。CG担当で、多方面に作品を発表されていましたが、３０代で帰らぬ人となりました。彼を星空へ誘ったけど、先にその世界へ旅たってしまった。有志の寄稿による追悼文集が配られ、思い出話が湧出。
Nさん，そこから眺める天の川はきれいでしょうね。安らかに眠れられんことを・・・合掌

若きケイロン・・・いて座

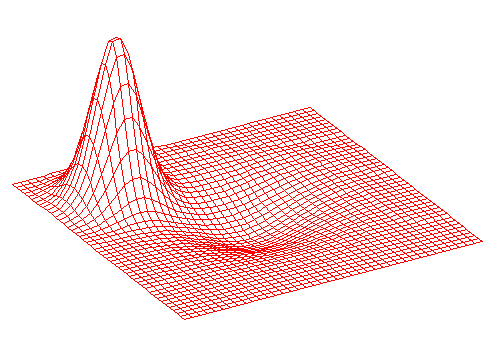
　gnuplot で下記のややこしい式を３D描画したもので，実は山が t の変化に伴って動くんです。
　ｘ，ｙ　-5～5　　ｔ　0～3
5*exp(-((x-t)**2+(y-t)**2))/4-0.2*exp(-(x**2+y**2)/4)
また．グラフを描くだけでなく，非線型方程式の解法，数値積分，微分方程式の解法，最小二乗法などの数値計算を行い，その結果を表示することもできます。詳しくは下記を
ぐにゅ
gnuplotで 続
gnuplotで

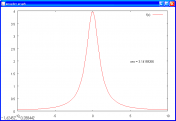
　定積分もできました。またもや図は薄すぎて見にくいですが
f(x)=4/(1+x*x) のグラフです。この関数は代数関数なのに積分するとarctan(x) になり，0から1まで積分するとπになることがわかっているので，種々の計算チェックに使われます。Simpsonの公式をちょっとだけ。
s=s+f(x)+4*f(x+h)+f(x+2*h);x=x+2*h;if(x＜x2) reread

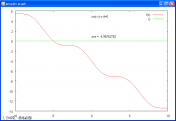
また微分方程式も解けました。RungeKuttaの式をちょっとだけ使って。グニュ君も成長しているが，やっぱり数値計算はScilabでやったほうがカンタンということがわかった。
コンパイラに頼り過ぎないで FreeSoft，OpenSource をもっと活用しましょう。

gnuplotで

　方程式が解けてしまった。gnuplotはもっぱら関数のグラフを描くツールと思っていたが、実はややこしい非線型方程式が解けます。
図は小さくて見にくいが sin(-x)-x-4=0 の解が x=-4.96762762452019と求まったというわけ。ちょっとだけニュートン法によるくり返し文を書いていますが。多分ほとんどの方程式は解けそうです。ただしＳｃｌａｂやOctoveの便利な関数は効かないみたいですが。→ここはAWさんにお聞きしたい
　さらに積分などもできるでしょう、これから考えてみよう。